Limites de suites et récurrence. Exercice 2.

Énoncé

Exercice bac 2

Soit la suite définie par  et pour tout entier naturel , par .

Si est la fonction définie sur l’intervalle  par alors on a, pour tout nombre entier naturel ,  . 

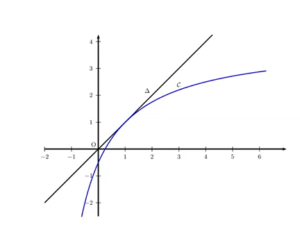
On donne en annexe (à rendre avec la copie) une partie de la courbe représentative de la fonction ainsi que la droite d’équation .

1. a) Sur l’axe des abscisses, placer puis construire , et en laissant apparents les traits de construction.

b) Quelles conjectures peut-on émettre sur le sens de variation et sur la convergence de la suite ?

2. a) Démontrer par récurrence que, pour tout nombre entier naturel , on a .

 b) Dans cette question, toute trace de recherche, même incomplète, ou d’initiative même non fructueuse, sera prise en compte dans l’évaluation.

Valider par une démonstration les conjectures émises à la question 1.b.

3. Dans cette question, on se propose d’étudier la suite par une autre méthode, en déterminant une expression de en fonction de .

Pour tout nombre entier naturel , on pose  .

a) Démontrer que la suite est une suite arithmétique de raison .

b) Pour tout nombre entier naturel , exprimer en fonction de .

c) En déduire la limite de la suite .