Vecteurs et colinéarité dans le plan

1- Notion de vecteur

a- Vecteurs du plan

Définition :

Soient et deux points distincts du plan. La translation qui transforme en est une transformation du plan qui à tout point associe le point tel que et ont même milieu.
Cette transformation est appelée translation de vecteur .

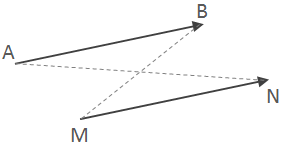
Définition :

Un vecteur est caractérisé par :
• Sa direction : la droite ou bien toutes les droites parallèles à .
• Son sens : de vers .
• Sa norme : la distance , notée .
Le point est l’origine du vecteur et le point est l’extrémité.
Le vecteur est appelé vecteur nul, noté .

Définition :

Les vecteurs et sont égaux lorsqu’ils ont même direction, même sens et même longueur.

Propriété :

Soient , , et quatre points du plan , revient à dire que le quadrilatère est un parallélogramme, éventuellement aplati.

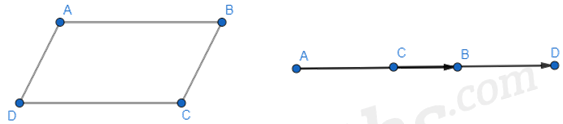
Le quadrilatère peut être nommé aussi :

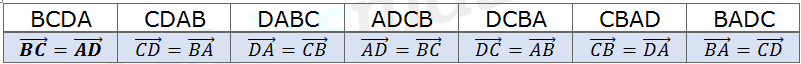
Définition :

L’opposé du vecteur est le vecteur , tel que .
et ont la même direction, la même longueur et un sens contraire.

Propriété :

Soient , et trois points du plan,
est le milieu de si et seulement si .

Propriété :

Soit un vecteur et un point du plan ,
il existe un seul point tel que .

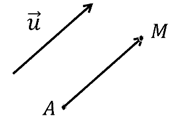
Remarques :

• signifie que .
• signifie que .

b- Somme de vecteurs

Définition :

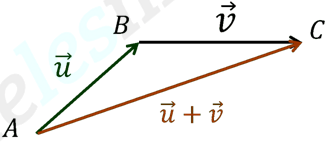
Soient et deux vecteurs.
La somme des deux vecteurs et est le vecteur associé à la translation
résultant de l’enchaînement de la translation de vecteur et la translation
de vecteur ;
On note .

Propriété :

Soient , et quatre points du plan ,
si et seulement si est un parallélogramme.

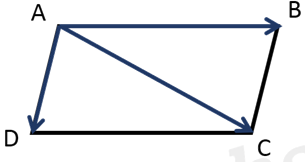
Si est un parallélogramme, on a aussi :
et

Théorème (Relation de shales) :

Soient et trois points distincts du plan. Alors : .

c- Coordonnées d’un vecteur

Définition :

Soient un repère et un vecteur.
On dit que deux réels et sont les coordonnées de vecteur , si et
seulement si .
On note :

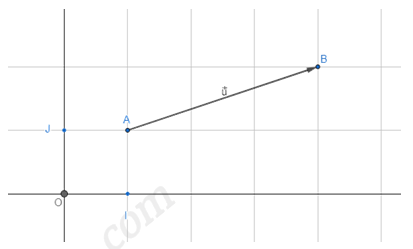
Exemple :

Dans cet exemple, on a :

Donc

Propriété :

Dans un repère , si et alors
On écrit aussi .

Exemple :

Soient et alors donc .

Propriétés :

Soient et , on a :
• si et seulement si
• .

Exemples :

Soient et alors donc .
Soient et un point tel que .
signifie que
c’est-à-dire
Donc .

Notation :

Si on pose et , le repère peut se noter

2- Colinéarité de vecteurs

Soit un repère orthonormé du plan.

a- Produit d’un vecteur par un réel

Propriété :

Soient un réel et un vecteur dans le plan,
Les cordonnées de sont .

Exemple :

Soient on a donc .

Propriétés :

Soient et deux vecteurs tel que .
• Si alors .
• Si alors et ont la même direction.
• Si alors et ont le même sens et
• Si alors et sont de sens contraire et .

Propriétés :

Soient et deux vecteurs et et deux réels, on a :
•
•
•
•
•

b- Colinéarité de vecteurs

Définition :

Soient et deux vecteurs non nuls,
On dit que et sont colinéaires si et seulement s’il existe un réel non
nul tel que .

Remarque :

Le vecteur nul es colinéaire avec à tout vecteur.

Propriété :

Soient et deux vecteurs non nuls,
et sont colinéaires si et seulement si leurs coordonnées sont proportionnelles.
C’est-à-dire il existe un réel non nul tel que et .

3- Applications

Soit un repère orthonormé du plan.

a- Déterminant

Définitions :

Soient et deux vecteurs,
Le déterminant des deux vecteurs et est un nombre réel noté ,
tel que .

Propriété :

Deux vecteurs et sont colinéaires, si et seulement si leur déterminant
est nul.

Exemple :

Soient et on a
Donc et sont colinéaires.

b- Parallélisme

Propriétés :

Soient et quatre points distincts deux à deux,
• si et seulement si et sont colinéaires.
• et sont alignées si et seulement si et sont colinéaires.

Exercice d’application :

Soient les quatre points et .
i- Est-ce que les points et sont alignées ?
ii- Est-ce que les droites et sont parallèles ?

Rédaction :

i- On a et
alors
alors et sont colinéaires, donc et ne sont pas alignées.
i- On a et
alors
alors et sont colinéaires, donc .