Dérivation

1- Nombre dérivé et tangente

Soient une fonction définie sur un intervalle de et sa courbe représentative dans un repère du plan.
Soient et un réel non nul tel que .

a- Limite à Nombre dérivé et taux de variation

Définitions :

On dit que est dérivable en s’il existe un réel tel que :
Le nombre est appelé le nombre dérivé de en , se note .
On a aussi si on pose .
Le nombre est appelé taux de variation entre et .
Si on pose et alors est le coefficient directeur de la droite .

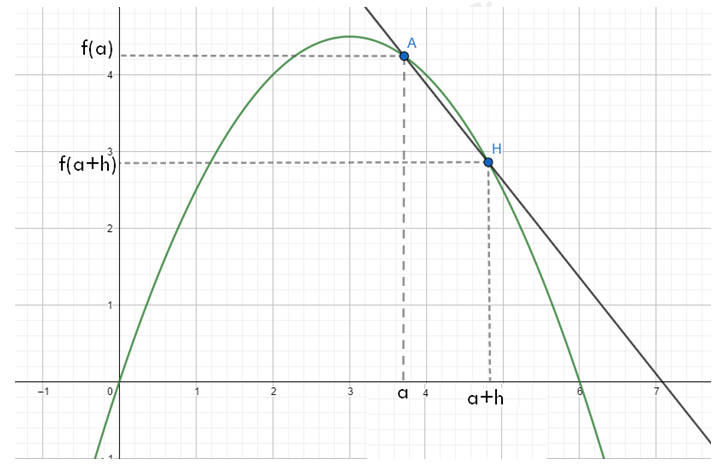
Le taux de variation s’appelle également le taux d’accroissement entre et .

Exemple :

Soit la fonction , et soit le point
On a

Donc est dérivable en et on a .

b- Tangente à une courbe

Définition :

Lorsque est dérivable en on appelle tangente à la courbe au point
d’abscisse la droite passant par le point dont le coefficient
directeur est le nombre dérivé .

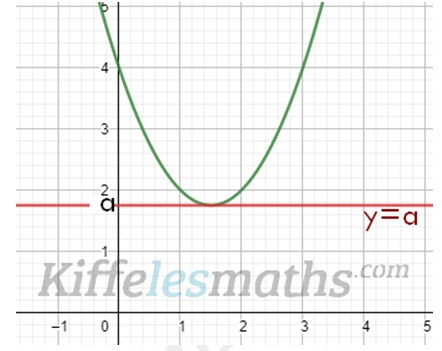
Remarque :

Lorsque alors la tangente horizontale à au point d’abscisse .
(elle est parallèle à l’axe des abscisses)

Exercice d’application :

Soit la fonction définie sur par
Montrer que admet une tangente en , en déterminant son coefficient directeur.

Rédaction :

On a
Donc est dérivable en et admet une tangente en de
coefficient directeur .

c- Équation de tangente

Propriétés :

Soit une fonction dérivable en
L’équation réduite de la tangente à la courbe de au point d’abscisse
est : .

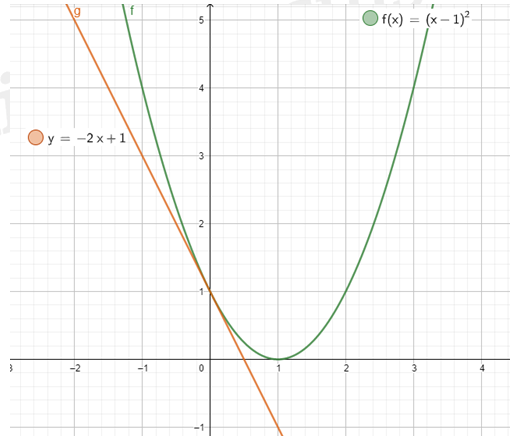
Exemple :

Soit la fonction définie sur par ,
D’après l’exercice d’application de la partie on a
L’équation de la tangente de en est : .
Donc : .

2- Fonctions dérivées

Soient une fonction définie sur un intervalle de et sa courbe
représentative dans un repère du plan.

a- Fonction dérivable

Définition :

On dit que est dérivable sur l’intervalle lorsqu’elle est dérivable en tout réel de .
On appelle fonction dérivée de la fonction qui, à tout réel de associe le réel On la note .

Exemple :

Soit la fonction , pour tout réels de on a :

Donc .

b- Fonctions dérivées des fonctions usuels.

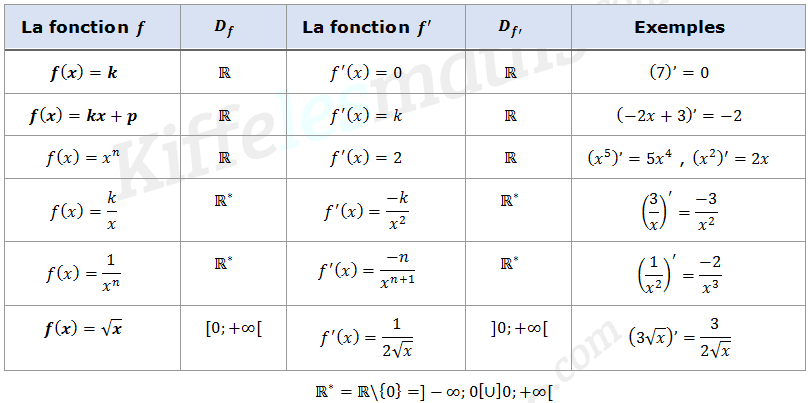
Propriétés :

Soient une fonction définie sur un intervalle et sa fonction dérivée sur , et soient et deux réels et , on a :

NOTATION :

Si alors se note .

c- Opérations sur les fonctions dérivées

Propriétés :

Soient et deux fonctions définies et dérivables sur un intervalle et et
deux réels, On a :