Vecteurs, droites et plans de l’espace
1- Vecteurs de l’espace :
a- Translation :
Définition :
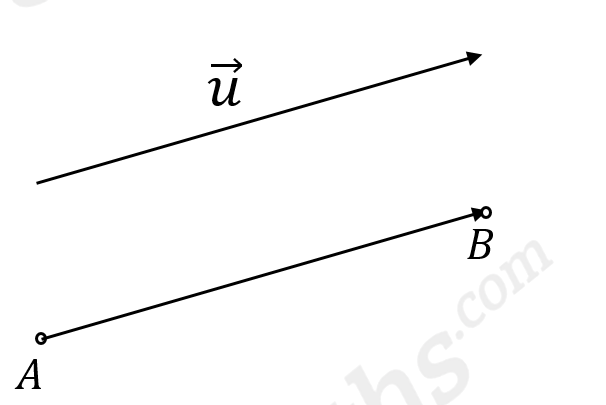
Soit un vecteur de l’espace.
est l’image de
par la translation du vecteur
signifie que
.
Remarques :
- On étend à l’espace la notion de vecteur étudiée en géométrie plane.
- La translation de vecteur
associe à tout point
l’unique point
tel que
et
ont même milieu.
- Si
et
les images respectives de
et
par une translation
du vecteur
dans l’espace alors on a
.
Conséquence :
- La translation conserve les distances c’est-à-dire si
et
sont les images respectives de
et
par une translation
du vecteur
dans l’espace alors
.
Voir les exercices d’application sur le site kiffelesmaths.com
b- Vecteurs colinéaires, vecteurs coplanaires.
Définition 1:
Soient et
deux vecteurs de l’espace.
et
sont colinéaires lorsqu’il existe un nombre réel
tel que
.
Remarques :
- On étend à l’espace la notion de vecteur étudiée en géométrie plane.
- La translation de vecteur
associe à tout point
l’unique point
tel que
et
ont même milieu.
- Si
et
les images respectives de
et
par une translation
du vecteur
dans l’espace alors on a
.
Propriétés :
Soient ,
et
trois points de l’espace deux à deux distincts.
Les points ,
et
sont alignés si, et seulement si, les vecteurs
et
sont
colinéaires, c’est-à-dire s’il existe un réel non nul tel que
.
Définition 2:
On considère quatre points distincts de l’espace ,
,
et
et soit
,
et
trois vecteurs définis par
,
et
.
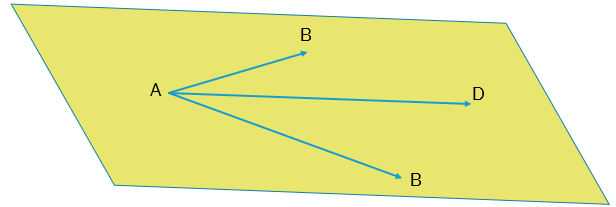
On dit que ,
et
sont coplanaires lorsque les points
,
,
et
appartiennent à un même plan. (c’est-à-dire
,
,
et
sont coplanaires).
Remarque :
- Le vecteur nul est toujours coplanaire à deux autres vecteurs quelconques
Propriété :
Soient ,
et
trois vecteurs non nuls de l’espace tels que
et
ne sont pas
colinéaires.
Les vecteurs ,
et
sont coplanaires si, et seulement si, il existe deux nombres réels
et
tels que
et on dit que
est une combinaison linéaire de
et
.
Applications et méthodes sur le site kiffelesmaths.com
c- Vecteurs linéairement indépendants et base de l’espace.
Définition 1 :
,
et
trois vecteurs de l’espace et
,
et
trois réels.
On dit que ,
et
sont linéairement indépendants lorsqu’ils ne sont pas
coplanaires, autrement dit lorsque .
Remarque :
Deux vecteurs non colinéaires sont linéairement indépendants.
Définition 2 :
Trois vecteurs linéairement indépendants forment une base de l’espace.
Notation :
La base formée par trois vecteurs ,
et
linéairement indépendants est noté
.
Propriété :
Soit une base de l’espace.
Pour chaque vecteur de l’espace il existe un unique triplet de réels
tel que
. Et on note
ou bien
.
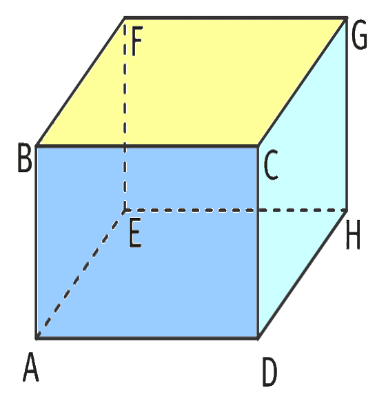
Exercice d’application :
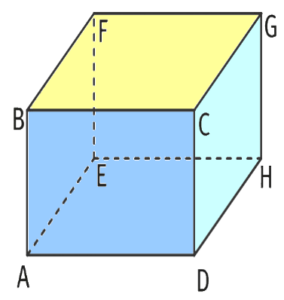
Soit un cube. “voir image”
i. Quel est l’image de par la translation du vecteur
? justifier.
ii. Est-ce que les vecteurs ,
et
sont coplanaires ? justifier.
iii. Déterminer le triplet tel que
.
Correction :
i. est un carré alors
, donc l’image de
par la translation du vecteur
est
.
ii. donc
,
et
sont coplanaires.
iii. .
iv. donc est le triplet associer au vecteur
dans la base
de l’espace.
2- Droites et plans de l’espace.
a- Droites de l’espace.
Définition 1 :
Soient un point et
un vecteur non nul de l’espace.
L’ensemble des points de l’espace tels que
avec
, est une droite dirigée par le vecteur
.
est un repère de cette droite.
est un vecteur directeur de la droite.

est un vecteur directeur de la droite.
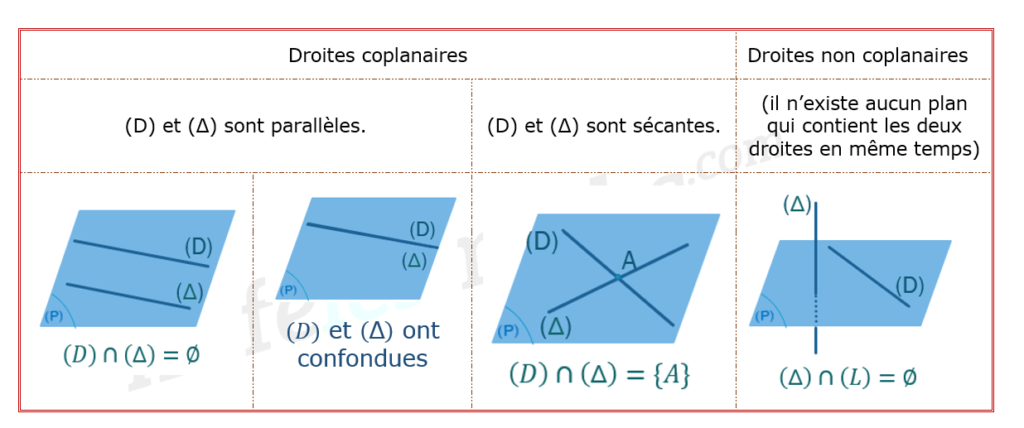
Définition 2 :
On dit que deux droites sont coplanaires, si elles appartiennent à un même plan.
Deux droites coplanaires peuvent être sécantes (avoir un point d’intersection) ou parallèles (strictement parallèles ou confondues).
Propriété :
Toutes les propriétés de la géométrie plane restent valables dans tout plan de l’espace, c’est-à-dire « lorsque les droites sont coplanaires, on retrouve les résultats obtenus en géométrie plane ».
Exemples
Soit un cube.
et
sont sécantes donc sont coplanaires.
et
sont parallèles donc sont coplanaires.
et
ne sont pas sécantes ni parallèles donc sont non coplanaires.
et
sont sécantes donc sont coplanaires.
b- Plans de l’espace.
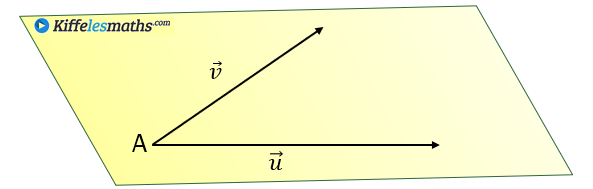
Définition 1 :
Soient un point de l’espace
et
et deux vecteurs non colinéaires de l’espace. L’ensemble des points
tels que
(avec
) est un plan de l’espace dirigé par la base
.
est un repère du plan.
La direction du plan est .
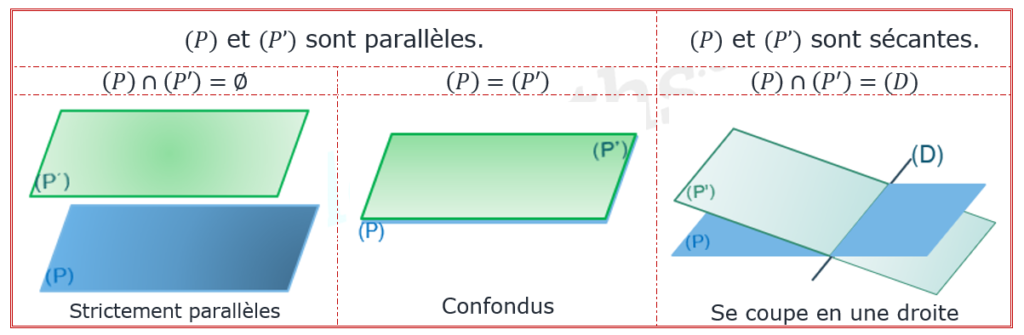
 Position relative de deux plans :
Position relative de deux plans :
Soient et
deux plans dans l’espace, on a trois cas possibles :
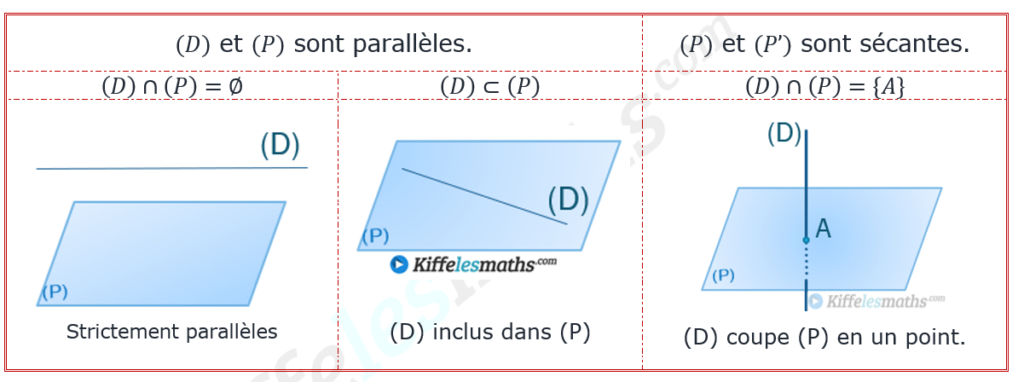
Position relative d’un plan et une droite :
Soient un plan et
une droite dans l’espace, on a trois cas possibles :
Remarque :
Trois points non alignés définissent un plan unique.
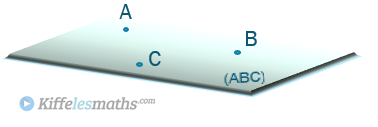
Exemples :
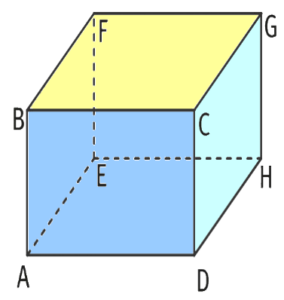
Soit un cube. “voir image”
- La droite
coupe le plan
en
.
- La droite
est inclus dans le plan
.
- La droite
est parallèle au plan
.
- Les deux plans
et
sont strictement parallèles.
- Les deux plans
et
sont sécantes en
.
- Les deux plans
et
sont confondus. (en fait c’est le même plan).
c- Parallélisme dans l’espace.
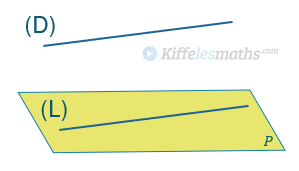
Théorème 1 :
Une droite est parallèle à un plan
si, et seulement si, il existe une droite
du plan
parallèle à
.
C’est-à-dire : Si alors
Théorème 2 :
Un plan est parallèle à un plan
si, et seulement si, il existe deux droites sécantes de
parallèles à deux droites sécantes de
.
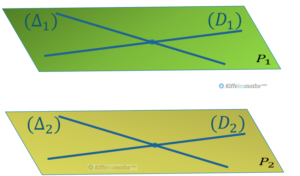
Exemple :
Soient et
deux droites sécantes dans le plan
;
et et
deux droites sécantes dans le plan
.
Si alors
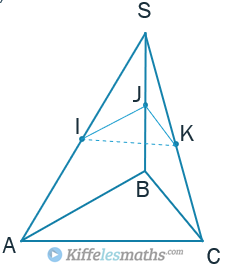
Exercice d’application :
Soit une pyramide
,
et
les milieux de
,
et
successivement.
Montrer que .
Correction :
On a et
deux droites sécantes dans le plan
et et
deux droites sécantes dans le plan
et puisque donc
Applications et méthodes sur le site kiffelesmaths.com
Théorème 3 :
Si deux plans sont parallèles, tout plan qui coupe l’un, coupe l’autre et les droites d’intersection sont parallèles.
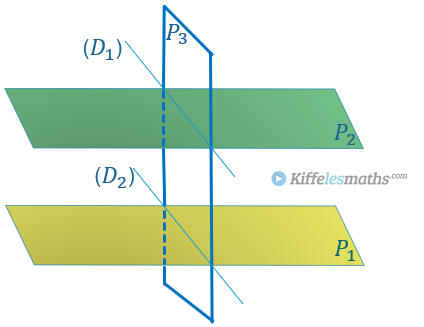
donc
Théorème 4 (Théorème du toit) (admis) :
Si deux plans sécants contiennent respectivement deux droites strictement parallèles, alors leur intersection est une droite parallèle aux premières.
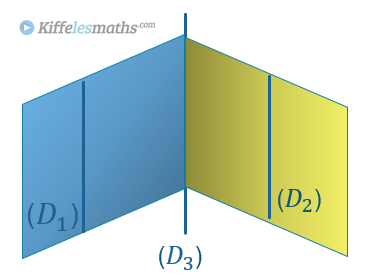
Dans cet exemple si alors
est parallèle avec
et
.
3- Repère de l’espace.
a- Coordonnées d’un point de l’espace.
Définition 1 :
Un repère de l’espace est défini par la donnée d’un point de l’espace et d’une base
de l’espace.
Notation :
Le repère défini par le point et la base
est noté
.
Définition 2 :
Soit un repère.
Pour tout point de l’espace, il existe un unique triplet
de
, tel que
.
,
et
sont les coordonnées de
dans le repère
.
est appelé abscisse de
,
l’ordonnée et
la cote.
Exemple :
Soit un cube et le milieu de
.
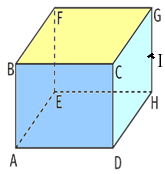
Déterminons les coordonnées de dans le repère
.
On a (relation de Chasles).
alors (
car
est un carré)
(
car
est un carré)
(
car
est un carré)
Donc les coordonnées de dans le repère
sont
.
C’est-à-dire .
Applications et méthodes sur le site kiffelesmaths.com
b- Opérations sur les coordonnées
L’espace est rapporté à un repère .
Propriétés :
Soit ,
et
trois points de l’espace tels que
,
et
le milieu de
, on a :
- Les coordonnées du vecteur
sont
est on écrit
- Les coordonnées du point
sont
est on écrit
.
Exemple :
Si et
alors
soit
.
Si est le milieu de
alors
soit
.
c- Représentation paramétrique d’une droite
L’espace est rapporté à un repère .
Propriété :
Soit une droite telles que
et
un vecteur directeur de
.
signifie qu’il existe un réel
tel que
.
Le système est une représentation paramétrique de la droite
.
Remarque :
Il existe une infinité de représentations paramétriques d’une droite.
Application :
Soit et
,
Déterminer la représentation paramétrique d droite
L’explication de tous le cours avec d’autres exemples et exercices en vidéo.
sur le site kiffelesmaths.com
